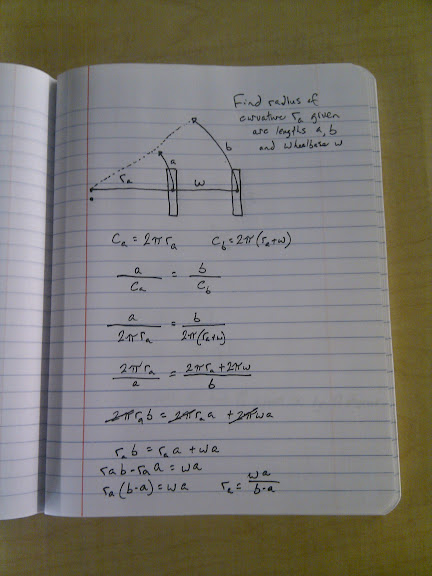
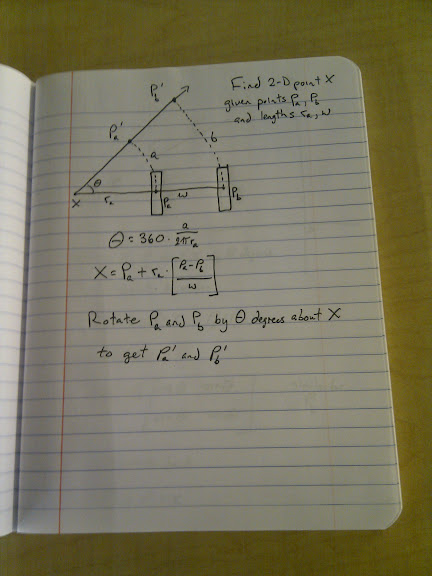
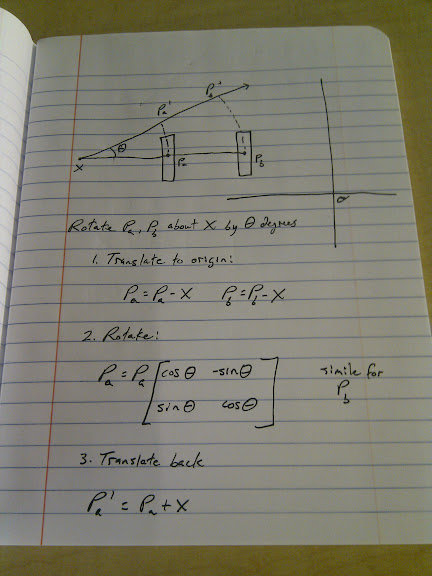
A few years ago my brother in law asked how pi is calculated, and we found that it can be done as a
reasonably intuitive algorithm, without any advanced math.
Ever since then, I've wondered if sines and cosines could also be calculated simply. Here's what I came up with. Please let me know if you know of a simpler way, where "simpler" means relying on fewer or more elementary mathematical principles.
Sines and cosines let us translate an angle in a right triangle into the length of one of is sides. But what is an angle? Well, on a unit circle, a 45 degree slice cuts off an arc that's 45/360ths the length of the circumference. We can cut that slice in half by finding the midpoint between the two ends of the arc, then extending that line out until it touches the edge of the circle. That slice represents 22.5 degrees. Since we have a point on the unit circle and we know its angle, the point's X and Y coordinates tell us the cosine and sine, respectively, of that angle. (And since the points are on a circle with a radius of 1, we know the hypotenuse of the right triangles is always of length 1).
Here's the same concept in pictures:


And here's python code that starts with the two points shown in the pictures, and keeps finding midpoints between them (recursively) until it gets a close enough approximation to any angle you want.
#!/usr/bin/python
"""
Released into the public domain, 12 June 2010
This program calculates the sine and cosine of an angle in a geometrically
intuitive way.
Here's how it works:
Start with a unit circle and observe that the points (1,0) and (0,1) on the
circumference of the circle are separated by 90 degrees.
The midpoint between those two points, (0.5, 0.5), bisects that 90
degree angle, forming two 45 degree angles. We can extend the line from
the origin through (0.5, 0.5) until it reaches the circumference of the unit
circle (that is, until its distance from the origin is 1), and we get
(0.707, 0.707). Thus we know that the cosine and sine of 45 degrees are both
0.707.
Likewise, we can find the cosine and sine of 22.5 degrees by taking
the midpoint between (0.707, 0.707) and (1,0), then scaling the line until
it reaches the circumference. And we can find the cosine and sine of
67.5 degrees by taking the midpoint between (0.707, 0.707) and (0, 1).
We can continue to bisect angles until we get arbitrarily close to any
angle we choose. The allowable angular error is set below as MAX_THETA_ERROR.
Note that this method is agnostic to the angular units we use. If we start off
by telling the program that (0,1) and (1,0) are separated by an angle of 90,
then the program will return a result measured in degrees.
If instead we say that (0,1) and (1,0) are separated by pi/2, we'll get a
result in radians.
"""
import math
MAX_THETA_ERROR=0.01
def cos_sin(theta, x1,y1,theta1, x2,y2,theta2):
"""cos_sin returns the (cosine,sine) of a value within MAX_THETA_ERROR
units of theta, given two points (x1,y1) and (x2,y2) that live
at angular posisions theta1 and theta2 on the unit circle. theta,
theta1 and theta2 must all have the same kind of angular unit (degrees,
radians, etc.), but this function doesn't care what that unit is or
how many of them make up a circle.
theta2 must be greater than theta1, and (x1,y1) and (x2,y2) must be
points on the circumference of the unit circle, less than 180 degrees
apart.
for example, cos_sin(30.0, 0.0,1.0,0.0, 1,0,0.0,90.0) returns
(0.866089312575, 0.499889290387), which are the cosine and sine of 30.
"""
# Uncomment this to see the successive approximations
#print "target: %.2f. (%.2f, %.2f)=%.2f (%.2f,%.2f)=%.2f" % \
# (theta, x1, y1, theta1, x2, y2, theta2)
# if one of the points is close enough to theta, we're done!
if (abs(theta1 - theta) < MAX_THETA_ERROR):
return (x1,y1)
if (abs(theta2 - theta) < MAX_THETA_ERROR):
return (x2,y2)
# the midpoint is just the average of the two points
x_midpoint = (x1 + x2) / 2.0;
y_midpoint = (y1 + y2) / 2.0;
# scale (x_midpoint,y_midpoint) by 1/midpoint_length to get a point
# exactly 1 unit away from the origin
midpoint_length = math.sqrt(x_midpoint*x_midpoint + y_midpoint*y_midpoint)
x_midpoint = x_midpoint / midpoint_length
y_midpoint = y_midpoint / midpoint_length
# the midpoint bisects the angle between the two points
theta_midpoint = (theta1 + theta2) / 2.0;
# figure out which side of the midpoint our target value theta lives on,
# and bisect the extended midpoint with one of the original points to get
# closer to the target
if (theta >= theta_midpoint):
return cos_sin(theta, x_midpoint, y_midpoint, theta_midpoint, x2, y2, theta2)
else:
return cos_sin(theta, x1, y1, theta1, x_midpoint, y_midpoint, theta_midpoint)
angle = 30.0
(cosine, sine) = cos_sin(angle, 1.0,0.0,0.0, 0.0,1.0,90.0)
print "The cosine of %.2f is %.2f" % (angle, cosine)
print "The sine of %.2f is %.2f" % (angle, sine)